ModExp Gas Cost
相关视频
正文
Simple Summary
Defines the gas cost of the ModExp (0x00..05) precompile.
Abstract
To accurately reflect the real world operational cost of the ModExp precompile, this EIP specifies an algorithm for calculating the gas cost. This algorithm approximates the multiplication complexity cost and multiplies that by an approximation of the iterations required to execute the exponentiation.
Motivation
Modular exponentiation is a foundational arithmetic operation for many cryptographic functions including signatures, VDFs, SNARKs, accumulators, and more. Unfortunately, the ModExp precompile is currently over-priced, making these operations inefficient and expensive. By reducing the cost of this precompile, these cryptographic functions become more practical, enabling improved security, stronger randomness (VDFs), and more.
Specification
As of FORK_BLOCK_NUMBER, the gas cost of calling the precompile at address 0x0000000000000000000000000000000000000005 will be calculated as follows:
def calculate_multiplication_complexity(base_length, modulus_length):
max_length = max(base_length, modulus_length)
words = math.ceil(max_length / 8)
return words**2
def calculate_iteration_count(exponent_length, exponent):
iteration_count = 0
if exponent_length <= 32 and exponent == 0: iteration_count = 0
elif exponent_length <= 32: iteration_count = exponent.bit_length() - 1
elif exponent_length > 32: iteration_count = (8 * (exponent_length - 32)) + ((exponent & (2**256 - 1)).bit_length() - 1)
return max(iteration_count, 1)
def calculate_gas_cost(base_length, modulus_length, exponent_length, exponent):
multiplication_complexity = calculate_multiplication_complexity(base_length, modulus_length)
iteration_count = calculate_iteration_count(exponent_length, exponent)
return max(200, math.floor(multiplication_complexity * iteration_count / 3))
Rationale
After benchmarking the ModExp precompile, we discovered that it is ‘overpriced’ relative to other precompiles. We also discovered that the current gas pricing formula could be improved to better estimate the computational complexity of various ModExp input variables. The following changes improve the accuracy of the ModExp pricing:
1. Modify ‘computational complexity’ formula to better reflect the computational complexity
The complexity function defined in EIP-198 is as follow:
def mult_complexity(x):
if x <= 64: return x ** 2
elif x <= 1024: return x ** 2 // 4 + 96 * x - 3072
else: return x ** 2 // 16 + 480 * x - 199680
where is x is max(length_of_MODULUS, length_of_BASE)
The complexity formula in EIP-198 was meant to approximate the difficulty of Karatsuba multiplication. However, we found a better approximation for modelling modular exponentiation. In the complexity formula defined in this EIP, x is divided by 8 to account for the number of limbs in multiprecision arithmetic. A comparison of the current ‘complexity’ function and the proposed function against the execution time can be seen below:
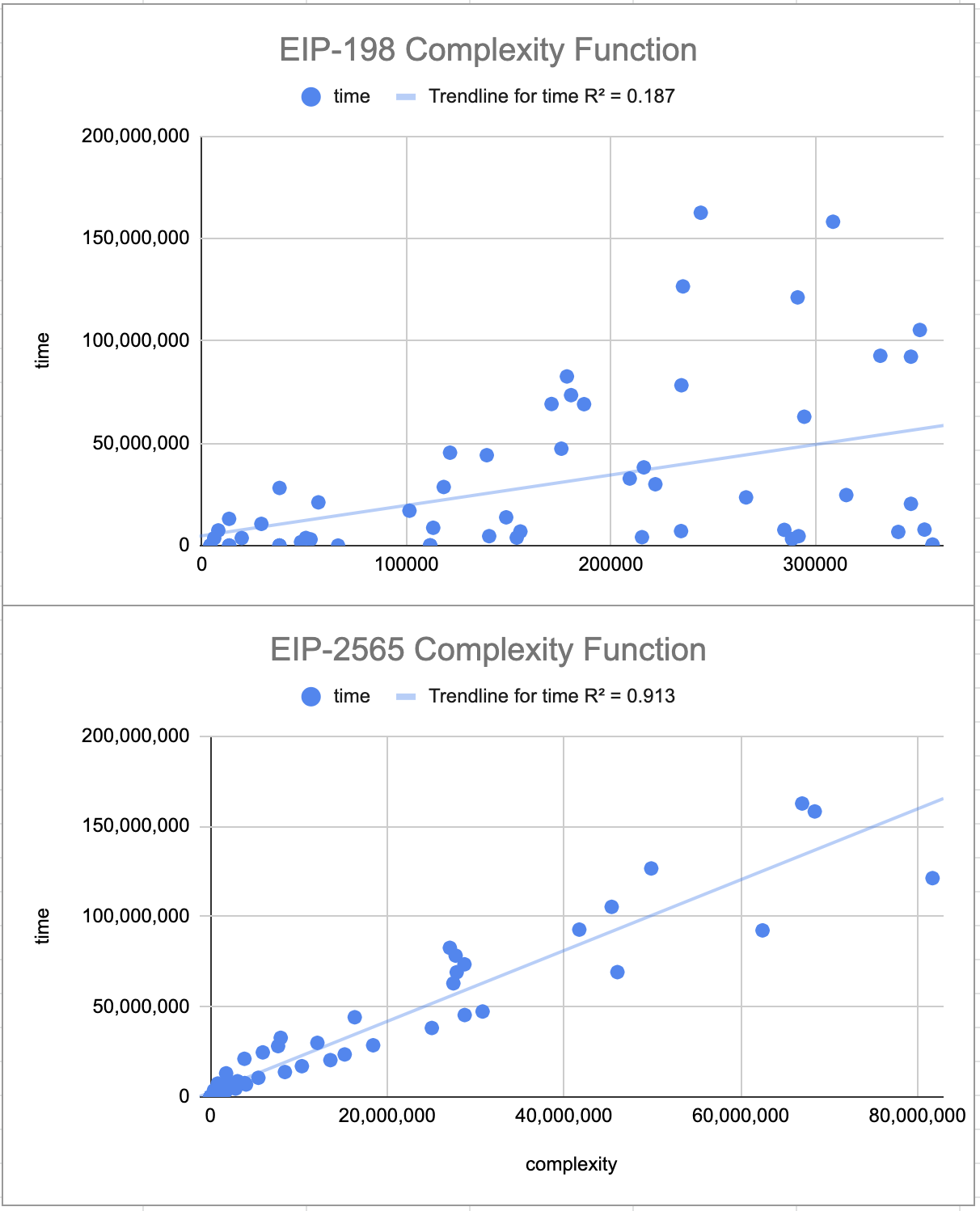
The complexity function defined here has a better fit vs. the execution time when compared to the EIP-198 complexity function. This better fit is because this complexity formula accounts for the use of binary exponentiation algorithms that are used by ‘bigint’ libraries for large exponents. You may also notice the regression line of the proposed complexity function bisects the test vector data points. This is because the run time varies depending on if the modulus is even or odd.
2. Change the value of GQUADDIVISOR
After changing the 'computational complexity' formula in EIP-198 to the one defined here it is necessary to change QGUADDIVSOR to bring the gas costs inline with their runtime. By setting the QGUADDIVISOR to 3 the cost of the ModExp precompile will have a higher cost (gas/second) than other precompiles such as ECRecover.
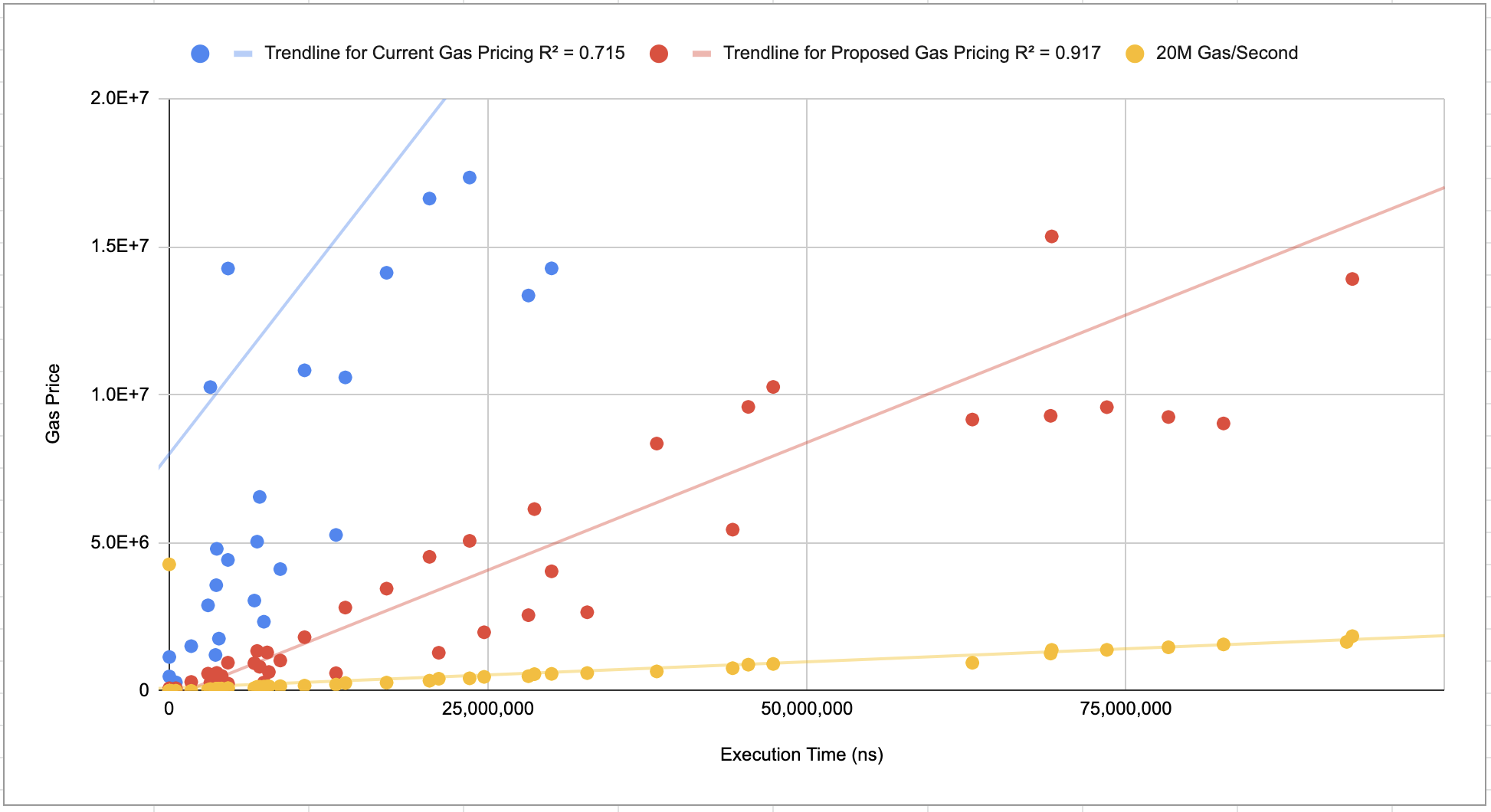
3. Set a minimum gas cost to prevent abuse
This prevents the precompile from underpricing small input values.
Test Cases
There are no changes to the underlying interface or arithmetic algorithms, so the existing test vectors can be reused. Below is a table with the updated test vectors:
| Test Case | EIP-198 Pricing | EIP-2565 Pricing |
|---|---|---|
| modexp_nagydani_1_square | 204 | 200 |
| modexp_nagydani_1_qube | 204 | 200 |
| modexp_nagydani_1_pow0x10001 | 3276 | 341 |
| modexp_nagydani_2_square | 665 | 200 |
| modexp_nagydani_2_qube | 665 | 200 |
| modexp_nagydani_2_pow0x10001 | 10649 | 1365 |
| modexp_nagydani_3_square | 1894 | 341 |
| modexp_nagydani_3_qube | 1894 | 341 |
| modexp_nagydani_3_pow0x10001 | 30310 | 5461 |
| modexp_nagydani_4_square | 5580 | 1365 |
| modexp_nagydani_4_qube | 5580 | 1365 |
| modexp_nagydani_4_pow0x10001 | 89292 | 21845 |
| modexp_nagydani_5_square | 17868 | 5461 |
| modexp_nagydani_5_qube | 17868 | 5461 |
| modexp_nagydani_5_pow0x10001 | 285900 | 87381 |
Implementations
Security Considerations
The biggest security consideration for this EIP is creating a potential DoS vector by making ModExp operations too inexpensive relative to their computation time.
References
Copyright
Copyright and related rights waived via CC0.